LCS(최장 공통 부분 수열)

최장 공통부분 수열이란?

주어진 두 문자열 사이에서 순서는 같지만 연속적일 필요는 없는 가장 긴 공통부분 수열을 찾는 문제이다.

즉, 두개의 문자열이 공통된 순서대로 존재하는지를 확인하는 알고리즘이다.

---

사용하는 이유

기존 반복문을 사용해 문자열 X와 Y의 모든 부분 수열을 찾으려면 각각 O(2^m)과 O(2^n)의 연산이 필요하며,

이 경우 전체 시간복잡도는 O(4^n)으로 매우 오래 걸린다.

하지만 LCS(Longest Common Subsequence) 알고리즘을 사용하면 문제를 O(m * n)의 시간복잡도로 해결이 가능하다.

---

접근방법(탑다운)

1. 포인터를 사용해서 문제 해결

문자열 A의 포인터 aIndex, 문자열 B의 포인터 bIndex를 사용하며 이동하면서 문자열을 비교한다.

초기 포인터

 

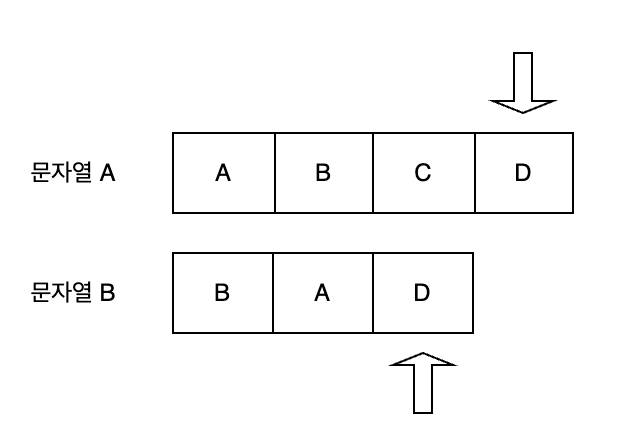
2. 문자열 비교

• A [aIndex]와 B [bIndex]가가 같은 문자라면:
  • 해당 위치는 공통부분 수열의 일부이므로 LCS(i-1, j-1) + 1의 결과를 사용.
  • 두 포인터를 모두 하나씩 줄여 재귀적으로 다음 위치를 비교합니다.

두개의 포인터 동시 감소

• A[aIndex]와 B[bIndex]가 다른 문자라면:
  • LCS(aIndex-1, bIndex): A의 포인터만 줄이는 경우
  • LCS(aIndex, bIndex-1): B의 포인터만 줄이는 경우두 가지 경우를 고려해 더 큰 값만 취합니다.
  • 이 중 최대값을 선택해 부분 문제의 최적 해를 찾으면 정답이다.

A 포인터 감소/ B포인터 유지

A 포인터 유지 / B포인터 감소

 

---

알고리즘 실전

https://www.codetree.ai/missions/2/problems/longest-common-sequence?&utm_source=clipboard&utm_medium=text

코드트리 | 코딩테스트 준비를 위한 알고리즘 정석

 

 

import java.util.*;
import java.io.*;

public class Main {
    static String A,B;
    static int[][] dp;

    public static void main(String[] args) throws IOException{
        simulate();
    }

    private static void simulate() throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        A = br.readLine();
        B = br.readLine();

        //A의 문자열 길이, B의 문자열길이
        dp = new int[A.length()][B.length()];
        for(int i = 0; i < A.length(); i++) {
           Arrays.fill(dp[i],-1);
        }

        int result = dfs(A.length()-1,B.length()-1);

        System.out.println(result);
    }

    private static int dfs(int aIndex, int bIndex) {
        if(aIndex <0 || bIndex<0) {
            return 0;
        }

        if(dp[aIndex][bIndex]!=-1) {
            return dp[aIndex][bIndex];
        }


        dp[aIndex][bIndex] = 0;

        char aCh = A.charAt(aIndex);
        char bCh = B.charAt(bIndex);

		// 같은경우
        if(aCh == bCh) {
            int result = dfs(aIndex-1,bIndex-1);
            dp[aIndex][bIndex] = Math.max(dp[aIndex][bIndex],result+1);
        }else { // 다른경우
            int left = dfs(aIndex-1,bIndex);
            int right = dfs(aIndex,bIndex-1);

            int max = Math.max(left,right);
            dp[aIndex][bIndex] = Math.max(dp[aIndex][bIndex],max);
        }

        return dp[aIndex][bIndex];
    }
}